He’s not an authority, he’s demonstrated his knowledge already in the past. Not taking the time to answer you in some drawn out manner doesn’t mean he’s wrong.
1 Like
WELL, this is literally a function of Cl=f(Cd). So with the Kmax. Your L will be the maximum for the current Cdmin value Or Clopt/Cdmin
@Aetreus If you want an L/D graph for the grid fins and monoplane wing. Unfortunately, there is no such schedule. Only Kmax
There’s a difference between “brief” and “wrong.” BBCRF’s responses were wrong. Just like, flagrantly wrong.
Well that sucks for you because as I have noted, Kmax is not enough to describe an air to air missile’s drag behavior. Because unlike an aircraft(or cruise missile), the missile will constantly vary in speed and therefore lift required to maintain level flight, and therefore its actual K in flight will not be Kmax. And of course lofting will throw a whole extra grenade into this because it means lift required isn’t just gravity, and at any rate the fins aren’t generating most of the lift to keep the missile in the air, only to control its AoA.
1 Like
Well yeah, you can see it on the charts. Lower Cl for all angles of attack. Meaning you’d need to pull more AoA for the same lifting force. But guess what? Through L/D(Cl), despite pulling more AoA Doing so wouldn’t mean a high loss in velocity. And up to what angle? <~20°. And from your own words, they don’t pull that much.
The force required to rotate them to those angles, I don’t give damn. Pretty sure they can do it.
Holy moly.
Do you even know what the direction of THAT hinge moment measure is? Do you know what the direction of the moment of the drag force is? Please tell us. Tell us
Do you need a drawing?
No you haven’t. You just quote M1.3 without any variables which depend on lots of stuff which YOU DON’T KNOW. How do I know? Because you didn’t answer this!
Not relevant? Lmao. Do you know what happens when there’s a higher pressure in-infront of the grid fins?
Nor you answer this
You are so damn high on an erroneous idea you are failing to ask yourself basic questions and if you do, you just try a way to justifying them with mental gymnastics.
8 Likes
I understand what you want to see.But the Kmax reflects the aerodynamic perfection of the aircraft. In Belotserkovsky’s Book there are graphs for an abstract lattice with different steps and for numbers M
3 Likes
I think one of the funniest parts of this whole “planar fins vs lattice fins” argument is the fact that despite graphs demonstrating the high drag issues of the lattice fins, and the (generally) better L/D ratio of planar fins, and the NATO paper specifically stating their high wave drag discredits their use for air to air missiles, the pro-russian players cannot or will not grasp the concept of these fins having pretty clear drag issues
The lattice fins do offer more lift at lower AOA’s, they also offer vastly more drag at all AOA’s according to the graphs.
Lets go for an example:
For a CL of 0.4, the planar fins deflect to roughly 12.5deg vs the lattice’s 8-9deg
At said AOA’s, the lattice fins Cd is roughly 150% that of the planar ones:
Which is how the planar fins exhibit better L/D ratio for given CL’s up to around 0.6, such as at 0.4 as seen in the graph:
The fact that the lattice fins can deflect less for a given amount of lift is a definite advantage for them, but does not change the fact that for fin deflections of up to (roughly) 12.5 deg for the lattice fins, and 20 deg for the planar fins, the planar fins are simply more effective designs.
ie: the R-77 should retain its energy better relative to lift at high fin deflection (12.5 deg and above) than the planar fin deflected above 20 deg AOA, but in all fin deflections below those points, the planar fins are more aerodynamically efficient.
Beyond this point, theres still the fact that the devs have not modelled the lattice fins drag to be unique in any way as it should be, which means that, as stated a while back, lattice fins are getting all their advantages in-game with none of their disdvantages.
This is further supported by the fact that though the R-77 and AIM-7M have almost identical sizes, with he 7M being slightly longer, the R-77 has been given a substantially lower CxK of 1.85 vs the 7M’s 2.3:
So, congrats to the pro-russian players, you’ve once again managed to weasel your way into an ahistorical buff. Its basically an artform how good you guys are at getting free handouts at this point
14 Likes
2 Likes
Your arguments are completely broken down by this graph
I don’t see the advantage of 150% of a conventional steering wheel
2 Likes
Already beaten. Get a better graph.
7 Likes
This graph is more than enough for understanding aerodynamic perfection
If it’s not enough for you. The Cd and Cl of the grid wing, frame and honeycomb structure are shown here. We are interested in cellular
1 Like
Translate
The plans of the lattice wings, appropriately
shaped, allow for smooth flow around the angles of attack
40-50°. At supersonic speeds, the lattice plans can be
placed close enough to each other without their mutual influence
and obtain a large total area of the lattice wing in a small
volume. Therefore, the lifting force of a lattice
wing turns out to be several times greater than the lifting force of a monoplane
wing with equal volumes: at M = 4, the lifting force of the lattice
is about 3 times higher than the lifting force of the corresponding
monoplane wing.
1 Like
Well, I wouldn’t be so sure. Remember that CxK is a parameter of the whole missile. And normally CxK increases for smaller missiles, we don’t know why but presumably Gaijin’s modeling makes it so somehow. AMRAAM has 1.6 CxK versus 1.85, despite being smaller, so it is a lot less draggy ingame. Testing and the ingame DLZ give it longer range than R-77, that’s why @MiG_23M is whining about needed performance improvements. The real loser is PL-12.
These are not lift and drag coefficients, these are axial and normal force coefficients. I am not doing a bunch of work to convert them, do that yourself if you want to present it as evidence.
This is about compactness, how much wing area you can fit in a given volume. Interesting for internal carriage or maybe inside a missile tube with folding fins, but not relevant.
3 Likes
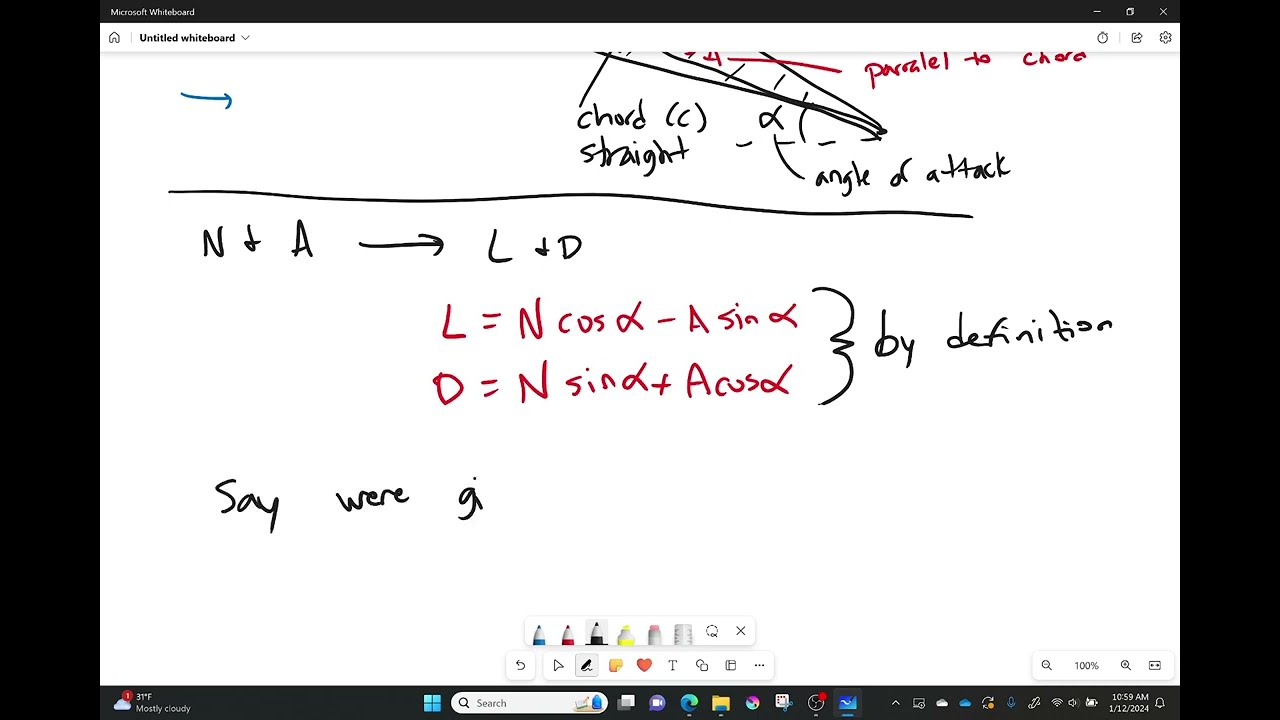
These are the coefficients of lift and drag
Сy-normal Force
Cx-axial Force
This Сya and Cxa
Small problem: In WT, its unlikely the R-77 will be hitting M4.0, or staying near M4.0 for any extensive period of time. Heres a test for example where when fired from M1.0 at 7550m, it reaches a peak of ~M2.85 (hard to tell exact number due to the clutter of all the missiles)
Even worse, when the missile goes active, its already sitting at M2.07:
and its impact velocity is around/below M1.3 (ie: the transonic regime where grid fins should be providing their highest drag):
and this is just for a 40km shot:
Secondly, nobody has said that lattice fins provide inferior lift, its pretty clear by the graphs already covered that they provide superior lift at lower AoA than planar fins. What HAS been said is that they tend to produce excessive drag, making them less efficient up until a certain AoA.
As I had already stated in the past, the modelling of the lattice fins to have the same drag profile as planar fins in WT specifically is vastly more advantageous to the R-77, which in all likelihood should actually be performing even worse than it does in-game due to the flight altitudes and speeds involved in normal combat.
This isn’t anything new though, as missile mechanics are almost always favorable to Russian missiles in WT. The best example of this being the missile diamond appearing when the motor is burning, no matter the type of smoke trail the missile makes. This is clearly disadvantageous to long burn and low smoke motors (common in NATO weapons). Another clear advantage of this is gaijin only modeling single plane maneuverability, advantageous for Russian missiles such as the R-27ER and its 35G skid-to-steer guidance, disadvantageous to the Magic II or AIM-54’s and any other missile using combined plane guidance.
7 Likes
You just do not get it. How do you model missile aerodynamics if you don’t understand that normal/axial coeffients are different from lift/drag coefficents.
Aerospaceweb.org | Ask Us - Lift & Drag vs. Normal & Axial Force
4 Likes
I’m not interested in how it’s done in the game. I didn’t see much resistance on the chart than a regular wing
1 Like
I already gave you these coefficients to be stupid enough.
Сy=Cyacos AoA-Cxasin AoA-Normal Force
Cx=Cxaсos AoA+Cyasin AoA-Axis Force
This is a graph of the normal and Axis force from the angle of attack
1 Like
Except, thats not true at all… Heres the AIM-120A vs R-77 for example:
Just about every single stat effecting flight is different. Their autopilots and seekers are pretty similar though:
The missiles are all similar in performance because theyre all missiles trying to resolve a similar problem with similar dimensions. The MICA, R-Darter, PL-12, and Derby are also their own unique missiles. Here’s the 120A vs PL-12 for example:
Don’t lie to handwave legitimate arguments
3 Likes
because R-33 and R-37/M developed for conformal ventral suspension on MiG-31.
( MiG-31M (closed project ) can carry up to 6 R-37 ( first version ) )
6 R-37
MiG-31BM up to 4 R-37M.
Given that they have enough spacing for the massive mid body wing, I don’t think the folded Grid fin (which will have much smaller diameter) can’t be carried in conformal ventral suspension