- Yes
- Yes, with BR changes
- No, with comments
I started this suggestion on the old forum but that is no longer available, so I’m restarting it here.
This initially started as something for uncapped, solid AP but I believe it can be used for APCHE and APCR. I’m still working on Soviet APHE.
I’ll start with solid, uncapped AP again and more or less copy what I posted on the old forums.
My suggestion is to modify the current armor penetration calculator to better represent AP performance. With the adoption of the formula system, the performance of AP and APC rounds were made uniform, disregarding historical documentation. While this has reduced the work to implement new rounds and eliminated debates about penetration standards. The downside is specific round performance is no longer historical. The issue is further compounded by the use of standard slope modifiers. The slope modifiers come from WWII Ballistics, Armor and Gunnery. They are dependent on the penetration data from the same source. The issue starts with how Gaijin implemented its formula. Instead of calculating the necessary theoretical penetration for the standard WWII BAG slope modifiers to work, Gaijin attempted to account for certain AP rounds shattering. The “shattered” vertical penetration is reduced from the theoretical penetration of the round. When that reduced vertical penetration is applied to the standard slope modifiers, the sloped performance of the round is also reduced. In many cases, the shattered vertical penetration performance is accurate, but the reduced sloped penetration is not. In other cases, the round did not shatter against vertical armor, so both its vertical and sloped penetration is incorrect. This issue can be addressed by removing the “shattering” modifier from the AP round version of the calculator and changing the K factor to 1800.
Based on work I have done for previous reports, I have been able to establish a few key factors in the AP formula. First, the formula uses a K factor of 1900. Second, the uncapped AP formula applies an additional .9x modifier to the result. That .9x modifier is to represent the shot shattering.
Here’s a screenshot of the formula results. First is the AP results, then the same round with the APCBC box check. AP is 175.20, APCBC is 194.67. 175.20/194.67 is .8999 or rounded up to .9.
Here is a screenshot of a Demarre calculator with the K factor set to 1900. In this version, the “a” variable is the K factor. As you can see, the standard result is 194.67, which is the APC result. The AP result is 175.20. Both results match the calculator results from Gaijin.
Spoiler

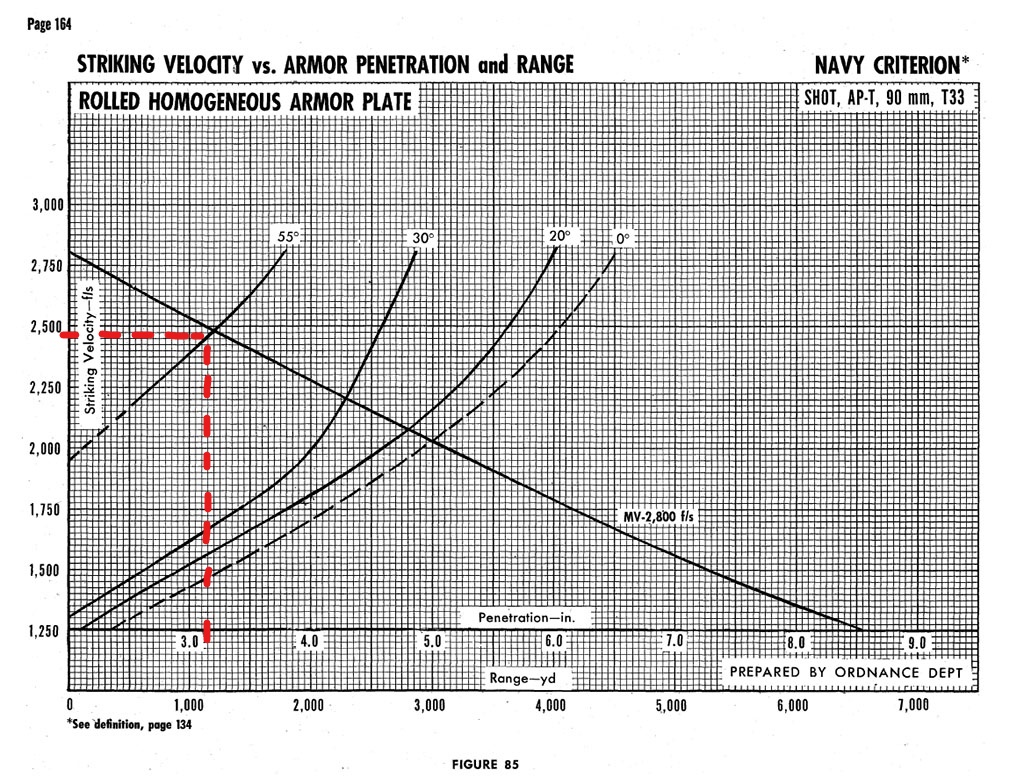
Next, we need to establish a basis for the 1800 K factor. I’ll use 90mm T33, since its a well documented round. The 90mm T33 will defeat the 80mm Panther glacis plate to roughly 1400 yards. This is shown by the following document. The penetration chart below shows the 90mm T33 will pen the 3.15" (80mm) at 55 degree glacis plate to about 2425 feet per second. The chart is based on US navy criterion, so the standard is pretty strict. Its a good basis for the performance of the round.
Using the in game armor protection analysis, we can see the Panther glacis equates to 171mm of protection against the 90mm T33.
Spoiler

Using the Demarre formula to change the penetration at 2425 fps to the muzzle velocity of 2800 fps, we get the following penetration.
Now, going back to our Demarre calculator, with the K factor set to 1800, we get the following results for 90mm T33 at 2800 fps.
Spoiler

To verify the results, we can look at another round. 57mm M70 AP is not prone to shattering, so we can use it as a good reference. The navy criterion chart is below.
Spoiler
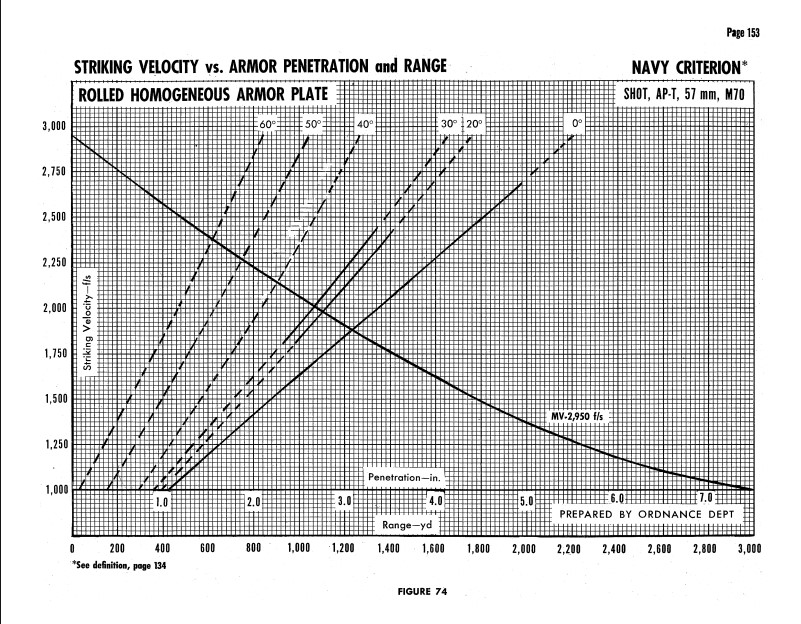
At its muzzle velocity, the M70 AP penetrates a little over 5.5" or 140mm of vertical armor. Using the 1800 K factor, we get the following result.
Spoiler

Roughly 142mm instead of over 140mm is close enough to call it good.
So, basically, I suggest removing the .9x modifier for uncapped solid AP and changing the K factor to 1800.