so you still dont know what the drag coefficent means
it is USED to calculate drag
BUT JUST BECASUE IT IS BIGGER DOSENT MEAN THAT THE DRAG IS BIGGER
becasue guess what, the su30 has a bigger area
tell me in what unit drag is measured
2 Likes
If the drag coefficient (Cd) of one aircraft is greater than that of another, it means that its drag increases more with speed than that of the other.
tell me in what unit drag is measured
and while you are at it take a physics class
https://www1.grc.nasa.gov/beginners-guide-to-aeronautics/drag-equation/
2 Likes
Cd (drag coefficient) = Cdo + kCl^2 where Cdo is the 0 lift drag (parasitic drag,skin friction drag) and kCl^2 is the induced drag.
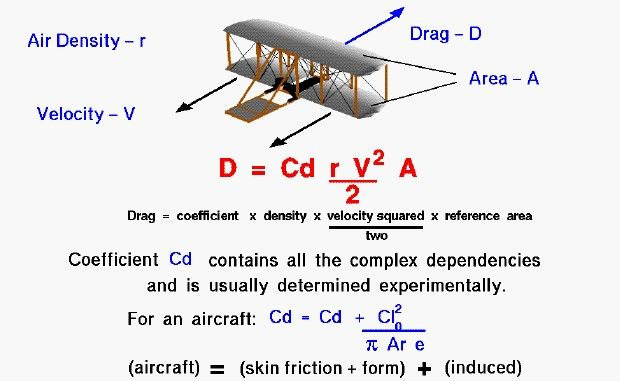
and Drag =
1 Like
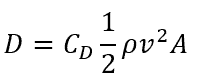
you dont even need to try it
he wont listen
It is possible for an aircraft with a lower drag coefficient to have a higher total drag if its area (S) is much larger or if it flies much faster.
This is not the case with the SU-30.
The formula you presented is correct for subsonic aircraft.
what is the unit of drag
tell me
1 Like
Newton or kgf
The drag coefficient now has no unit because it is dimensionless, as well as coef friction.
so tell me how this isnt showing the aircrafts drag then
and what is the size of a given aircraft doing?
it is almost like the size of an aircraft dosent corospond with the Cd0
becasue if it would you wouldnt need the surface of your object in the drag equasion
1 Like
If you don’t show me which parameters you selected in Stats Shark and don’t show what the other axis of the graph is about, it’s difficult to say anything definitive
provided it has the same shape/geometry.
A 1:1000 scale model of a Boeing 777 has the same C8 as the aircraft, but we are comparing a Su-30 and a J-10.
Size does have an indirect correlation with drag, yes, you’re either being intellectually dishonest or just plain misinformed.
While the actual drag is indeed not as exaggerated as some rumors suggest, Cdo assigned to the J-10C in the game is also set a bit high.
Specifically, considering that the J-10C and the Eurofighter Typhoon have similar fuselage lengths, the J-10C has a smaller cross-sectional area (due to its single-engine design) and features a more pronounced waist design. Therefore, the J-10C’s fuselage drag in the transonic regime should actually be lower overall than the Typhoon’s(And indeed, the same is true in the game.)
Taking the difference in reference area into account (37 m² vs. 51.4 m², excluding ailerons), the peak Cdo for the J-10C should be below 0.0194, whereas the current in-game value is 0.0204.
Furthermore, for the wing section, a more suitable reference for comparison is actually the JAS 39 Gripen, as they share similar sweep angles and canard positions. Considering that the J-10 lacks wingtip pylons and features a wingtip clipping design similar to the F-15, the wing Cdo of the J-10C should not exceed the Gripen’s peak of 0.0112, yet the current in-game value is 0.0123.
3 Likes
However, it’s unrealistic to expect Gaijin to adjust the J-10C’s FM. We cannot obtain real J-10 FM , and Gaijin does not accept this type of datamined or simulated data. Therefore, the only way to make the J-10C perform better at high altitudes while carrying the higher-drag and heavier load of 8x PL-12 missiles is to equip it with the WS-10B engine, either as a direct replacement or as a researchable modification.
4 Likes
This equation does not apply to supersonic aircraft. It cannot explain the phenomenon that objects surge in resistance at supersonic speed
1 Like
what is this supersonic formula that you talk about ? mind sharing it with us ?. the only difference is the way you calculate Cd but u still use the (calculated) Cd value in the Drag equation.
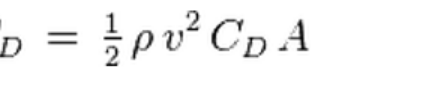
for supersonic wings the approximate formula
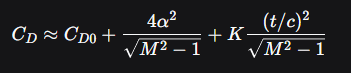
In which alpha is AoA.
M is Mach number.
t/cIt is the relative thickness of the profile.
and K is a constant that depends on the profile shape.
But in practice, the semi-empirical formula is used.
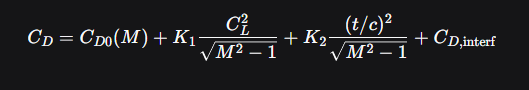
For supersonic fuselages, the theoretical minimum wave drag is given by the “Law of Areas” (Sears-Haack Rule).
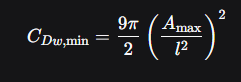
and where do u use that Cd ? in the same drag equation lmao
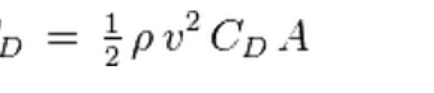
The J-10C engine is labeled S10B, but this is actually WS10B. Why does Gaijin refuse to acknowledge that it is WS10B?
4 Likes
Sorry for the delay in replying, I was traveling.
Do you think it’s useless circular logic, as if we were using the same formula to define and apply the variable.
There is a clear separation between its determination and application.
Cd is applied in the drag formula, but the calculation of Cd is done differently under supersonic and subsonic/transonic conditions.
If we use the same reference area, M=2.0, value of ρ = high altitude, ~11 km):
ρ≈0.364kg/m^3 (ISA). The only different parameter will be the calculation of Cd; if we use the subsoicna formula, Cd will be 0.04, while for Cdsup it will be 0.03.
Dsub=0.5×ρ×(680m/s) ^2 ×S×0.03 =126.235,2N
Dsup=0.5×ρ×(680m/s) ^2 ×S×0.04 = 168.313,6N
That’s a difference of 33.33%.
33% more fuel required
33% less range
Undersized engine power
i clearly stated previously that the Drag formula is the same but the way you calculate Cd changes. again you used the calculated Cd value in the drag equation but
you only get the value of Cdo
in this chart. Cd0 is not the same as Cd but a part of it.
Cdo is the zero lift drag coefficient (parasitic drag coefficient)
while Cd is the total coefficient of drag.
also how did you even calculate the value of Cd here ?
how did u get 0.03 ? 0.04 ?
without specifying the value of K =1/( πeAR) thus (AR , e) , Cl , wave drag etc
so where did you get these vales ?